
 |
||||||
 |
 |
|||||||||||||
|
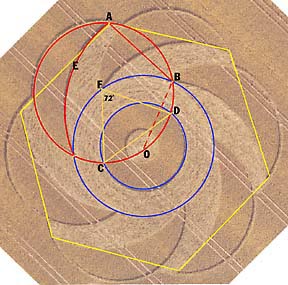
Andrews Catalog T482 This combines the side of a hexagon, OB, with the side of a pentagon, AB, to get the radius of circle 1, OA. From Ptolemy's theorem of chords, with G equal to the golden mean and OF=1, we can prove that: 20A= G+AB (square root 3), or OA= 1,82709. Therefore by Rule 2, circles 1 and 3 give a ratio of 3.338, note A in the second octave. By crop circle theorem 4 the hexagon circles 1 and 2 give a diatonic ratio of 4/3, note F. Is the raised circle a clue? D is the center of the arc of the crescent E. Angle CFD is 72 degrees, so CD is also the side of the pentagon. This example of mathematical art gives the same diatonics as T448, notes F and A2, but the design is better. The diatonic circles now go through the tips of the moon, not the center, and the accuracy is 0.1%, not the previous 0.5%. Artistic as it is, the pattern contains math, and no previous artist has used mathematics as a theme. Ptolemy's theorem of 150 AD is a prehistoric landmark, because it is the foundation of trigonometry. |
||||||||||||||
 |
||||||||||||||
|
T487 (Andrews Catalog) By rule 2, the area of the outer circle is four times the area of the inner circle, giving a diatonic ratio of 8/1, note C''', and letter C by the crop circle code. It is a double application of crop theorem 2, one equilateral triangle drawn inside another. (Note that due to angle of original photo, correction is slightly off- FS) Photo correction & diagrams © Freddy Silva 1997. Photos: T482 © Lucy Pringle, T487 © Steve Alexander.. Text © Gerald Hawkins.
Return to Part 1 of Latest Work Return to Part 2 of Latest Work |
||||||||||||||
 |
 |
 |
 |
|||||||||||
 |
||||||||||||||
 |
|||||||